data(COKMexico)
# Definimos nuestro objeto SpatFD
SFD_PM10_NO2 <- SpatFD(Mex_PM10, coords = coord_PM10, basis = "Fourier",
nbasis = 21, lambda = 0.000001, nharm = 2)
# Agregamos las observaciones de NO2 al objeto que creamos antes por medio del argumento add
SFD_PM10_NO2 <- SpatFD(NO2, coords = coord_NO2, basis = "Fourier",
nbasis = 27, lambda = 0.000001, nharm = 2,
add = SFD_PM10_NO2)
# Definimos los modelos de varianza de cada una de las variables
model1 <- gstat::vgm(647677.1,"Gau",23317.05)
model1 <- gstat::vgm(127633,"Wav",9408.63, add.to = model1)
# Especificamos la ubicación no muestreada
newcoords <- data.frame(x = 509926, y = 2179149)Cokriging
El cokriging es una extensión del kriging que permite predecir una variable en una ubicación no muestreada utilizando no solo datos de esa misma variable, sino también información de otras variables relacionadas o covariables. Este método aprovecha la correlación espacial entre varias variables para mejorar la precisión de las predicciones.
Supongamos que queremos hacer la predicción tomando en cuenta \(p\) variables de forma simultánea. Considerando \(Z(s_i) = (Z_1(s_i),Z_2(s_i),\cdots,Z_p(s_i))'\) , el predictor para \(Z_l(s_0), 1\leq l\leq p\) basado en p, basado en las \(p\) variables tiene la forma
\[ Z^*_l(s_0) = \sum_{i=1}^n \sum_{q=1}^p \lambda_{qi}Z_q(s_i) \]
El mejor predictor lineal insesgado de una variable en la ubicación \(s_0\) está dado por la minimización de
\[ max_{1\leq l \leq n}\{Var[Z_l(s_0)-Z^*_l(s_0)]\} \]
Por eficiencia computacional, puede decidirse minimizar
\[ \sum_{i=1}^nVar[Z_l(s_0)-Z^*_l(s_0)] \]
En el paquete SpatFD se realiza cokriging sobre los scores elegidos para todas las variables funcionales involucradas. Las predicciones de scores se utilizan para construir el predictor funcional del cokriging.
La función COKS_scores_lambdas nos permite hacer el cokriging funcional
cokrig = COKS_scores_lambdas(SFD_PM10_NO2, newcoords, model1)Using fill.all = TRUE by defaultUsing method = 'lambda' by default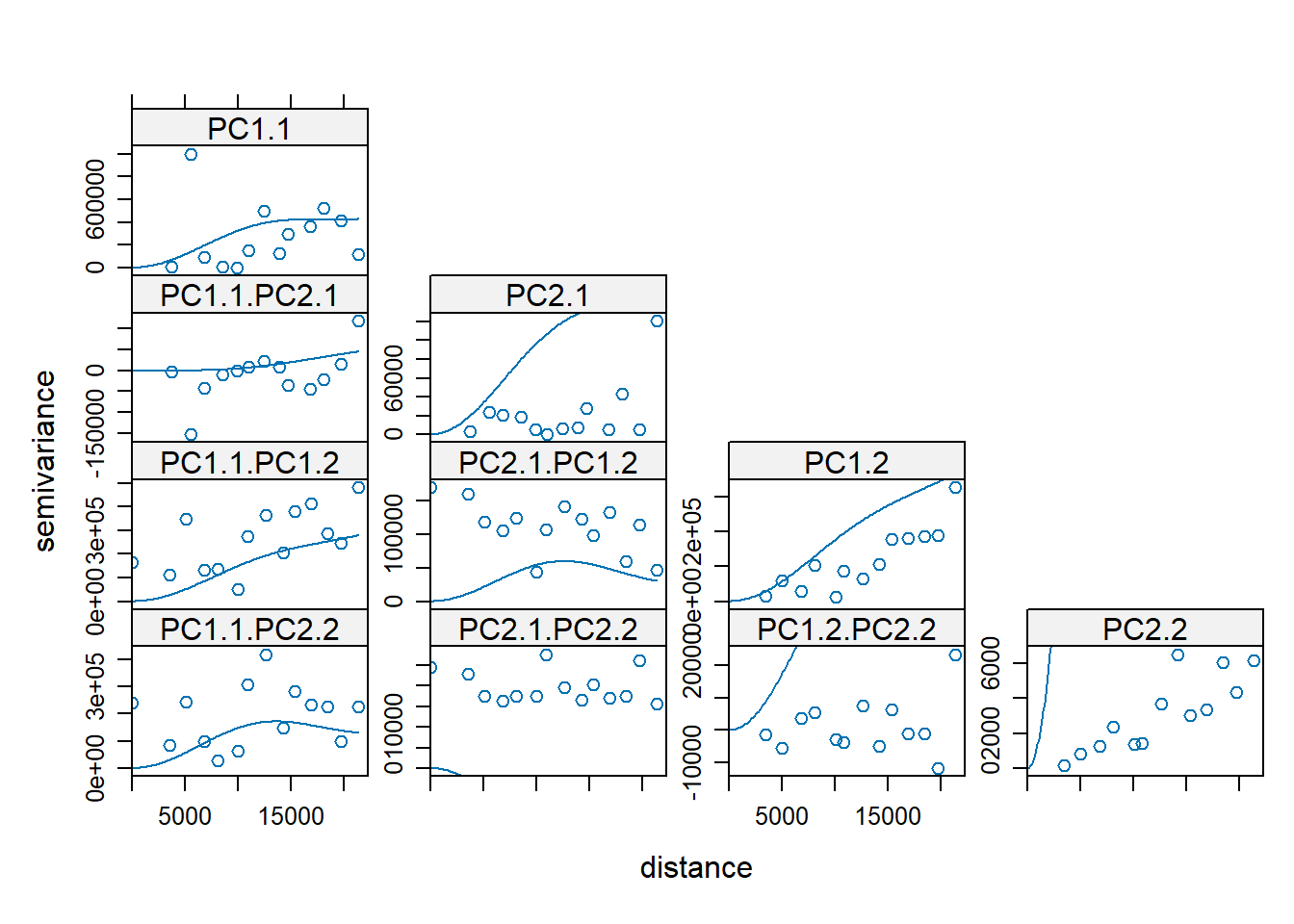
Linear Model of Coregionalization found. Good.
[using ordinary cokriging]cokrig$modelfitdata:
PC1.1 : formula = puntajes[[1]][[1]]`~`1 ; data dim = 13 x 2
PC2.1 : formula = puntajes[[1]][[2]]`~`1 ; data dim = 13 x 2
PC1.2 : formula = puntajes[[2]][[1]]`~`1 ; data dim = 18 x 2
PC2.2 : formula = puntajes[[2]][[2]]`~`1 ; data dim = 18 x 2
variograms:
model psill range
PC1.1[1] Gau 356886.232 23317.05
PC1.1[2] Wav 251618.187 9408.63
PC2.1[1] Gau 157275.294 23317.05
PC2.1[2] Wav 66770.748 9408.63
PC1.2[1] Gau 509628.594 23317.05
PC1.2[2] Wav 86045.557 9408.63
PC2.2[1] Gau 9178.223 23317.05
PC2.2[2] Wav 77729.767 9408.63
PC1.1.PC2.1[1] Gau 96771.742 23317.05
PC1.1.PC2.1[2] Wav -11290.879 9408.63
PC1.1.PC1.2[1] Gau 358697.498 23317.05
PC1.1.PC1.2[2] Wav 84592.302 9408.63
PC2.1.PC1.2[1] Gau -36478.239 23317.05
PC2.1.PC1.2[2] Wav 57029.144 9408.63
PC1.1.PC2.2[1] Gau 11668.546 23317.05
PC1.1.PC2.2[2] Wav 137897.759 9408.63
PC2.1.PC2.2[1] Gau -1677.278 23317.05
PC2.1.PC2.2[2] Wav -12680.551 9408.63
PC1.2.PC2.2[1] Gau 16583.870 23317.05
PC1.2.PC2.2[2] Wav 40857.282 9408.63