SpatFD
La geoestadística funcional es una extensión del marco teórico de la geoestadística tradicional, que permite el análisis y modelado de datos funcionales correlacionados espacialmente, tanto univariados como multivariados. Este enfoque incluye herramientas exploratorias, predicción espacial mediante kriging y cokriging, muestreo óptimo, clasificación supervisada y simulación. A través de este enfoque, se modela la estructura de dependencia espacial entre curvas, lo que permite realizar predicciones en ubicaciones no muestreadas utilizando predictores funcionales que minimizan las varianzas del error de predicción. Además, se ofrece la optimización de la configuración de las ubicaciones de muestreo para mejorar la predicción espacial funcional.
Las herramientas disponibles también permiten la representación gráfica de las curvas predichas en cada ubicación y el mapeo de las superficies en cada punto temporal. La clasificación supervisada integra la correlación espacial, y se extiende a escenarios con medidas funcionales repetidas en cada localización. Finalmente, la simulación de datos funcionales correlacionados espacialmente puede ser tanto condicional como incondicional, y se fundamenta en el supuesto de espacios de Hilbert conjuntos gaussianos.
Datos Funcionales
Imaginemos que estamos interesados en estudiar cómo varía la temperatura en diferentes ciudades del mundo durante un año completo. Para hacerlo, en lugar de tomar una sola medida de la temperatura, registramos el promedio mensual de la termperatura durante todo un año.
En lugar de analizar cada punto de temperatura de manera independiente, podemos ver la temperatura a lo largo del añi como una función continua del tiempo. Esta función nos describe cómo la temperatura cambia en cada instante del día, lo cual permite realizar análisis mucho más precisos.
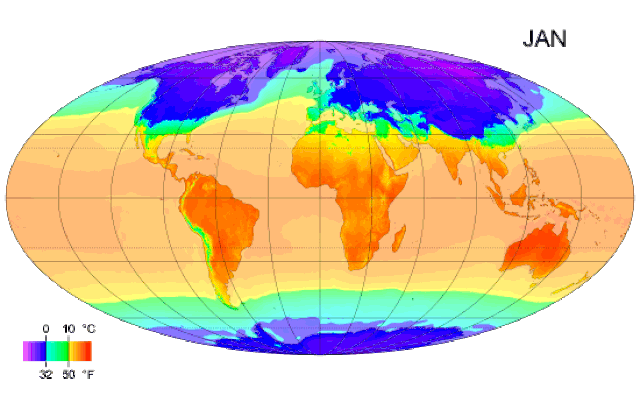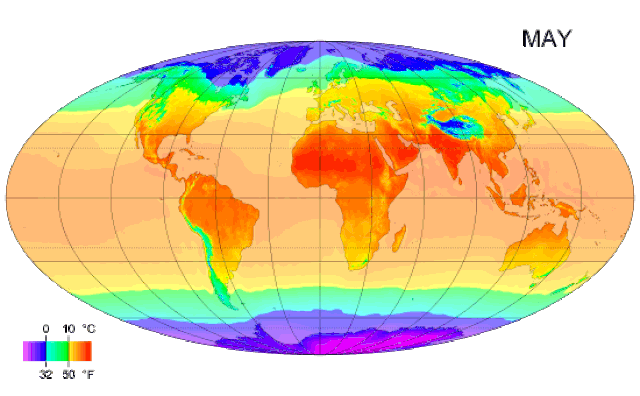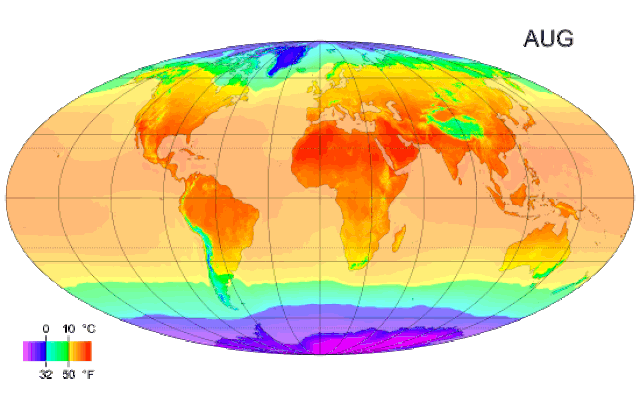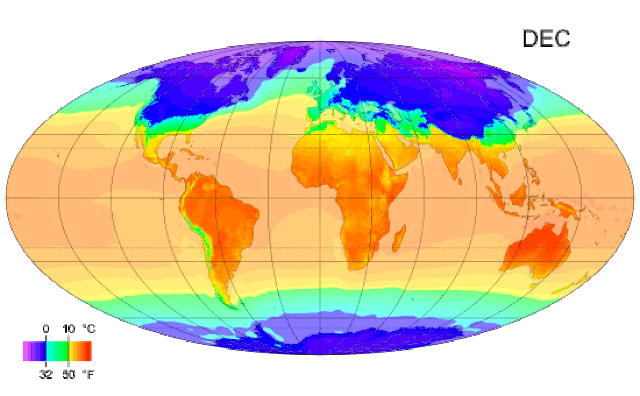
Los datos funcionales son los que en lugar de contemplar cada dato como una observación puntual, se consideran como funciones continuas observadas en un conjunto de puntos. Los datos funcionales permiten capturar mejor la complejidad de fenómenos que además de variar en el espacio, varían en dominios continuos como el tiempo o la altitud, además de facilitar la detección de tendencias o anomalías teniendo en cuenta múltiples dimensiones de variación.