# Load data and coordinates
data(AirQualityBogota)
#s_0 nonsampled location. It could be data.frame or matrix and one or more locations of interest
newcoorden=data.frame(X=seq(93000,105000,len=100),Y=seq(97000,112000,len=100))
# Building the SpatFD object
SFD_PM10 <- SpatFD(PM10, coords = coord[, -1], basis = "Bsplines", nbasis = 17,norder=5, lambda = 0.00002, nharm=3)
# Semivariogram models for each spatial random field of scores
modelos <- list(vgm(psill = 2199288.58, "Wav", range = 1484.57, nugget = 0),
vgm(psill = 62640.74, "Mat", range = 1979.43, nugget = 0,kappa=0.68),
vgm(psill =37098.25, "Exp", range = 6433.16, nugget = 0))Kriging
El Kriging es un método de interpolación basado en la teoría de procesos estocástocos que permite estimar los valores que toma una variable en lugares no muestreados a partir de la suposición de que las ubicaciones están correlacionadas espacialmente.
Kriging Ordinario
Dado un conjunto de observaciones en diferentes localizaciones \(s_1,s_2,\cdots,s_n\) busca predecir el valor de la variable de interés en una nueva ubicación \(s_0\) como una combinación ponderada de las observaciones:
\[ \hat{Z}(s_0) = \sum_{i=1}^n \lambda_iZ(s_i) \]
Donde \(\lambda_i\) son los pesos asignados a cada observación, determinados en función de la covarianza espacial entre \(s_0\) y \(s_i\) determinado por un variograma.
Kriging Funcional
En el contexto funcional, las observaciones en cada ubicación espacial no son valores discretos sino funciones completas. Supongamos que tenemos un conjunto de funciones \(X(s_1,t),X(s_2,t),\cdots,X(s_n,t)\) donde cada \(X(s_i,t)\) es una función que describe el comportamiento de la variable de interés a lo largo de un dominio continuo \(t\) (como el tiempo).
El kriging funcional extiende la idea del kriging clásico al predecir una función en una nueva ubicación \(s_0\) utilizando una combinación ponderada de las funciones observadas en las localizaciones \(s_1,\cdots,s_n\). En ese orden de ideas, podemos formular el kriging funcional de la siguiente manera
\[ \hat{X}(s_0,t)=\sum_{i=1}^n \lambda_i(t)X(s_i,t) \]
donde \(\lambda_i(t)\) son las funciones de peso que dependen de la localización y del dominio funcional \(t\). Estas funciones de peso se determinan resolviendo un sistema de ecuaciones basado en la covariancia entre las funciones observadas y la función a predecir.
Con el paquete SpatFD podemos crear un objeto SpatFD y definir los modelos de semivariogramas que vamos a emplear en el kriging. En este caso usaremos los datos AirQualityBogota y ajustaremos tres semivariogramas, uno wave, uno Mattern y por último un exponencial, la ubicación que queremos predecir se define en la variable newcoorden.
Existen dos enfoques diferentes para realizar el kriging funcional, el método de scores y el método lambda.
Método de Scores
En el método de scores, el análisis funcional se basa en una descomposición de las funciones observadas en un conjunto de componentes principales, generalmente a través de una descomposición en funciones base (como la descomposición en funciones ortogonales o en series de Fourier). Este método se descompone en dos etapas:
Descomposición funcional: Se aplica una descomposición funcional de las observaciones para representar cada función como una combinación de componentes principales (bases funcionales) y sus correspondientes coeficientes o “scores”. Si las funciones \(X(s_i,t)\) observadas se pueden representar como:
\[ X(s_i,t) = \sum_{k=1}^K \alpha_{ik}\phi_k(t) \]
donde \(\phi_k(t)\) son las bases funcionales y \(\alpha_{ik}\) son los scores de las componentes principales para cada localización \(s_i\). En lugar de predecir la función completa, este método se centra en predecir los scores en la ubicación no observada \(s_0\).
Predicción de una nueva ubicación: El kriging se aplica sobre los scores obtenidos. Se predicen los scores de la nueva ubicación \(s_0\) para construir la función predicha \(\hat{X}(s_0,t)\) como una combinación de las bases funcionales ponderadas por los scores predichos:
\[ \hat{X}(s_0,t) = \sum_{k=1}^K \alpha_{0k}\phi_k(t) \]
La función KS_scores_lambdas permite realizar el kriging usando este método al usar “scores” en la opción method
KS_SFD_PM10_sc <- KS_scores_lambdas(SFD_PM10, newcoorden, method = "scores", model = modelos)Using first variable by defaultUsing fill.all = TRUE by default[using simple kriging] [using simple kriging] [using simple kriging]Método Lambda
Este método utiliza una combinación de las funciones observadas, ponderadas por ciertos coeficientes o pesos, para estimar la función en la nueva ubicación, es decir, el kriging se lleva a cabo directamente sobre las funciones. El predictor \(\breve{\chi}_{ s_0}(t)\)
está dado por
\[\breve{\chi}_{s_0}(t)=\sum\limits_{i=1}^{n}\lambda_i\chi_{s_i}(t)\]
Deben encontrarse los pesos \(\lambda_i\) que minimicen la diferencia entre la verdadera función en la ubicación no observada \(s_0\) y el predictor. Eso se expresa matemáticamente como:
\[ min||\chi_{s_0}(t)-\breve{\chi}_{s_0}(t)||^2 \]
donde \(\chi_{s_0}(t)\) es la verdadera función en la ubicación \(s_0\). La minimización de esta expresión se realiza en el sentido de la norma \(L^2\).
La función KS_scores_lambdas permite realizar el kriging usando este método al usar “lambda” en la opción method
KS_SFD_PM10_l <- KS_scores_lambdas(SFD_PM10, newcoorden ,method = "lambda", model = modelos)Using first variable by defaultUsing fill.all = TRUE by default
Finalmente, ambos métodos pueden ser aplicados usanto “both” como argumento en method.
KS_SFD_PM10_both <- KS_scores_lambdas(SFD_PM10, newcoorden, method = "both", model = modelos)Using first variable by defaultUsing fill.all = TRUE by default[using simple kriging]
[using simple kriging]
[using simple kriging]Gráficamente
Podemos graficar las predicciones usando la función ggplot_KS
ggplot_KS(KS_SFD_PM10_both,show.varpred = FALSE,
main = "Plot 1 - Using Scores",
main2 = "Plot 2 - Using Lambda",
ylab = "PM10")[[1]]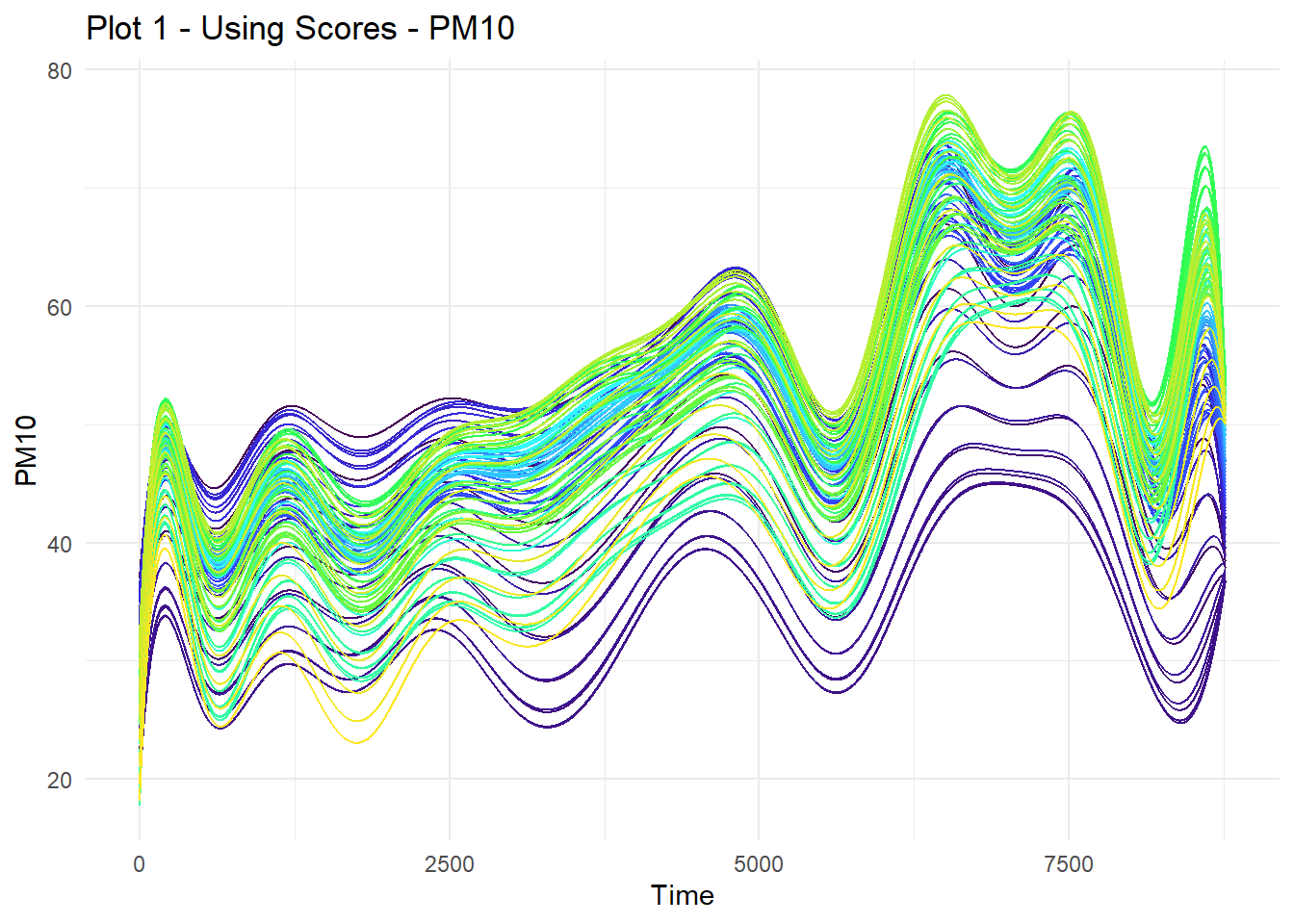
[[2]]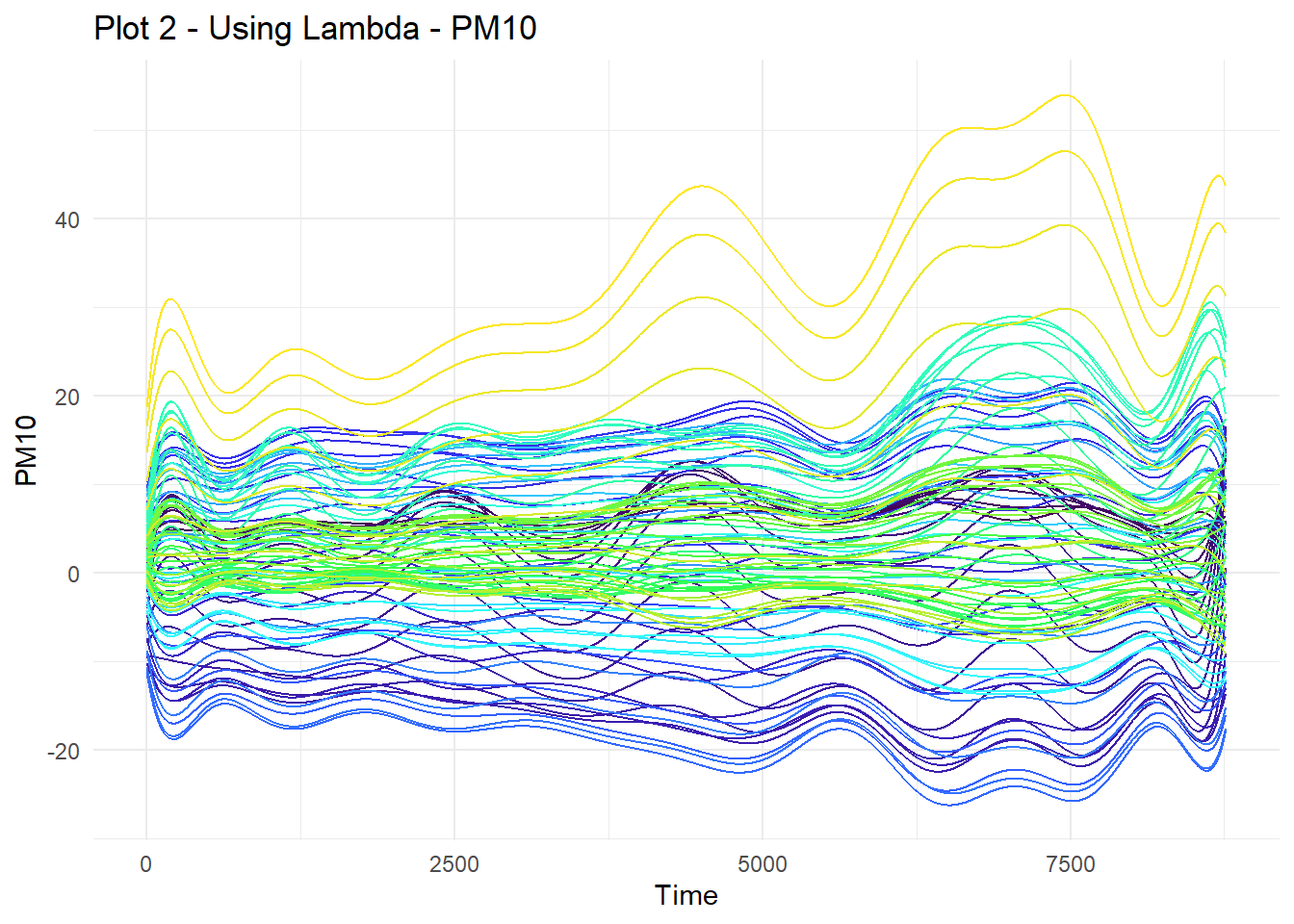
Así mismo, podemos graficar las predicciones suavizadas en tiempos específicos.
ggmap_KS(KS_SFD_PM10_both,
map_path = map,
window_time = c(2108),
method = "lambda",
zmin = 50)Using fill.all = TRUE by default[[1]]